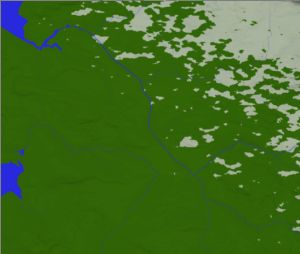
3. The next step is to build a river system for each continent. In the configuration, we can set the required number of river sources per romb as a function of the height of the romb’s vertices, as well as the spreading interval of the possible number of river sources. River data contains the coordinates of lattice nodes, as well as the height and streamflow at these nodes.
Creating rivers is one of the most difficult parts of the project. Here you can see how they look on a map.
4. Based on the previous steps, the calculations of the planet’s relief can be started. This is a long and arduous process that involves numerous sorting and smoothing steps. But, fortunately, this process can be divided into small separate subprocesses, in which only the data of a romb and rombs adjacent to it are involved. Therefore, efficient parallelization of computations can be achieved.
At the very end, an fBm mesh is built, which is modulated by the surfaces specified in the planet’s configuration. This forms the top layer of the planet’s relief (terrain).
The figure shows an example of a romb and rombs surrounding it, but already with the created relief.
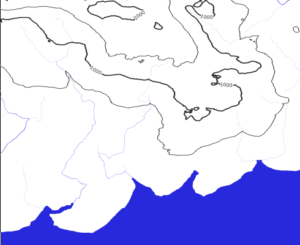
5. The local mesh of all rombs previously created is used to obtain the final geometries (GIS objects): boundaries of continents, lakes, rivers, and elevation contours.
An example of what elevation contours looks like. For a more detailed overview, turn on the star button in the Leaflet window and zoom in a map to the maximum.