The final relief of a planet is the composition of the water surface’s values and the terrain layer values, the later is the hill-layer data combined with some noise data preliminary deformed in a special way. This noise data is a noise defined on the rhombus domain. Here we will focus on the terrain layer creation in detail.
To deform the hill-layer, we create lower and upper bounds (surfaces), which will confine future terrain layer. The noise is scaled appropriately so that its values are within the bounds. The lower bound can be made negative, so that the terrain layer goes into the water surface, lowering it. But too large negative values lead to numerous local depressions in the relief, which may or may not be desirable. River channel level (or water surface level) is considered as zero level.
The noise data limited in this way are multiplied by the values from the hill-layer, and we get the terrain layer as a result.
Noise bounding surfaces
In general, we have to build bounding surfaces differently in the sea, in the land areas, and in the transition area between them. In the case of the sea, we can resort to planes for the bottom and top bounds. Planes are also suitable for the land areas, except for the river valleys. There we must use a special approach.
It is natural to use a parametrized function for the transition area from a river channel to far-from-river regions, so that the rise is gentle near the lowland rivers, and steep near the mountainous rivers. The project uses a sine wave function sin(π*x^a/2)^b,
where the parameter a can depend on the hill-layer value, parameter b can be different for different types of valleys, and x is a distance from the river channel. This gives lines (and surfaces) of varying steepness. We can apply the similar function to the transition area from the sea to the land.
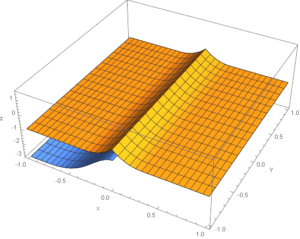
In the next diagrams, there are the upper and the lower bounding surfaces: brown is for the river, and blue is for the sea.
 |
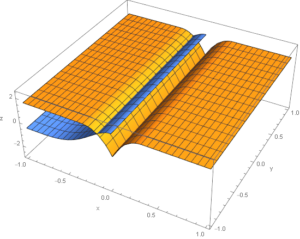 |
The river channel surface has a=0.5, which corresponds to mountainous terrain and greater steepness. The sea surface has a=2.0, which gives a gentle coast.
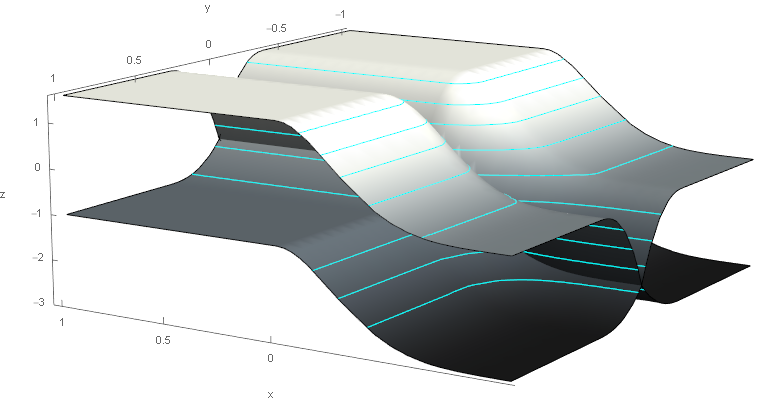
In the case when a river flows into the sea, we must combine these surfaces. Here are the lower bounding surface of the river mouth.
Here are the upper bounding surface of the river mouth.
And finally, if all combined in one, we get the space between the bounding surfaces in which the noise values are located.
For this demonstration, I use the case where the upper and lower surfaces touch at the river channel. But it is possible to make a gap between them, then it will turn out that the river crosses some hills or rocks. Also, parameter b equals 2 everywhere.
Terrain configuration
All constructions in the previous section can be defined with Terrain element. For Devil in the Ring planet it is as following.
<Terrain raise_min_add="100">
<RombNoise lat_ai_min_level="1" lat_ai_max_level="7" scaling="1.0" fractalH="0.52" ifp1="7" ifp2="3"/>
<NoiseDeform bottom_limit="-0.25" top_limit="1.0" ampl_smooth_steps="8">
<Sea zone="0.9">
<Bottom z_bound="-2.0" surface="\x->(sin $ (pi::Double)*x/2)"/>
<Top z_bound="-0.1" surface="\x->(sin $ (pi::Double)*x/2)"/>
</Sea>
<Gulf zone="0.6">
<Bottom z_bound="-2.0" surface="\x->(sin $ (pi::Double)*x/2)"/>
<Top z_bound="-0.1" surface="\x->(sin $ (pi::Double)*x/2)"/>
</Gulf>
<River zone="0.5">
<Bottom z_bound="-3.0e-2" surface="\x->(sin $ (pi::Double)*x/2)**1.0"/>
<Top z_bound="-3.0e-2" surface="\x->(sin $ (pi::Double)*x/2)**0.8"/>
</River>
</NoiseDeform>
</Terrain>
On this planet a=1 and the shapes of river valleys are the same for any altitude, but the depth of valleys is different because of different hill-layer values.
In addition to the sea and the land, we also have parameters for the gulfs (not any gulfs, but special ones). zone attribute defines the influence distance of a river or the sea on the land territory (the size of the romb edge is 1.0).